Sorts

Sorting 5000 items from least to greatest.

Big O notation is used to indicate complexity and the amount of time to complete the sort.

Insertion Sort

static void insertionSort(int arr[])
    {
        int n = arr.length;
        for (int i = 1; i < n; ++i) {
            int key = arr[i];
            int j = i - 1;

            while (j >= 0 && arr[j] > key) {
                arr[j + 1] = arr[j];
                j = j - 1;
            }
            arr[j + 1] = key;
        }
    }

Linear algorithm that sorts by finding the insertion point of the next number for sorting in the proper order.

It has two nested loops, which means that as the number of elements n in the array arr grows it will take approximately n * n longer to perform the sorting. Represented by O(n^2).

Bubble Sort

public static void bubbleSort(int arr[]) {
        int len = arr.length;
        for (int i = 0; i < len - 1; i++) {
            for (int j = 0; j < len - i - 1; j++) {
                if (arr[j] > arr[j+1]) {
                    int temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                }
            }
        }
    }

Bubble Sort is the simplest sorting algorithm that works by repeatedly swapping the adjacent elements if they are in wrong order. Often takes a long time since it needs multiple runs to sort the items in the correct order.

Selection Sort

public static void selectionSort(int arr[]) {
        int len = arr.length;
        for (int i = 0; i < len - 1; i++) {
            int mindex = i;
            for (int j = i+1; j < len; j++) {
                mindex = j;
            }
            int temp = arr[mindex];
            arr[mindex] = arr[i];
            arr[i] = temp;
        }
    }

A linear sort algorithm that runs through the data, finds the smallest value and puts it at the end. It takes multiple runthroughs to put the data into the right order.

Merge Sort

public static void mergeSort(int arr[], int start, int end) {
        if (end > start) {
            int mid = (start + end) / 2;
            mergeSort(arr, start, mid);
            mergeSort(arr, mid + 1, end);
            gather(arr, start, mid, end);
        }
    }

A divide and conquer algorithm. The array is split into two, where data is compared. The data is reordered appropriately and put into one array again afterwards.

Since the merge sort divides the data and calculates smaller sets of data at once, its time complexity is O(n log(n)), making it more efficient than the previous sorts.

Efficiency Analysis

I performed analysis on these 4 different sorts by running them under different amounts of data, ranging from 1000 to 10000, then graphing the nanoseconds it took to complete the sorting. Below is a graph of all the sorts compared on one graph. 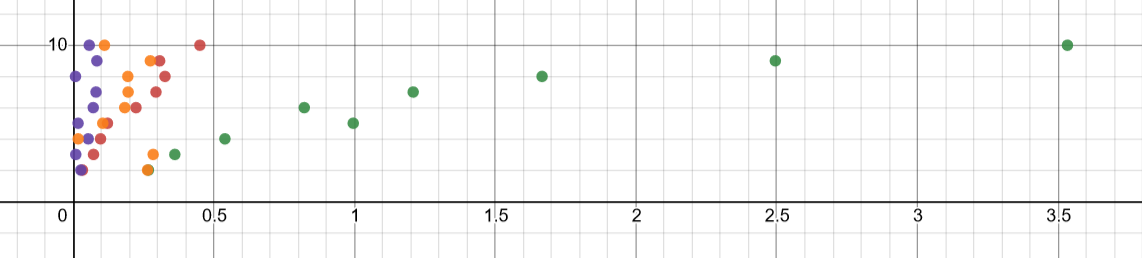Red: Insertion Green: Bubble Purple: Selection Orange: Merge

According to the distribution of the graph, the selection sort seems to be the optimal method for sorting these sets of data. From least to most efficient: bubble, insertion, merge, then insertion.

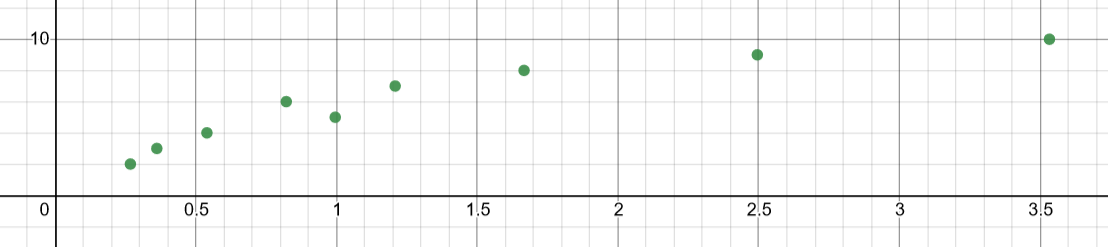
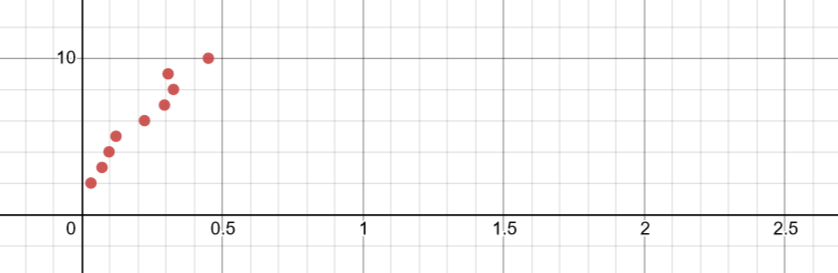
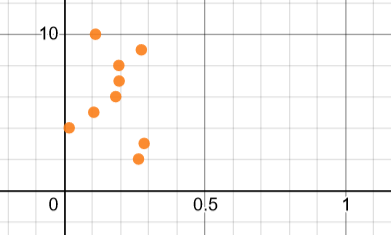
However, after doing research, most pages have stated that merge sorting is the most effective type of sort. Issues in my analysis could be that I didn’t use large enough data sets or didn’t collect a large enough range of data. Overall, we can state that the selection sort is most optimal for this size and type of data, but for other data types and sizes, the same may not be true.

Replit	Review Ticket
Replit	Review Ticket